Disclaimer: Everything I write here are notes taken while watching this online course by Colt Steele.

Introduction to a problem

Let's say that there's a problem.

Write a function that accepts a string input and returns a reversed copy of said input

There will be multiple solutions here. There might be even 10! However, how do we know which solution is the "best" solution. Is there some kind of "measurement" when evaluating the quality of solutions?

To explain the quality of code, humans came up with a numeric representation, the Big O. Instead of saying "this code is good" or "this code is bad", we can refer to the numeric evaluation of Big 0.

Timing our code

Suppose we want to write a function that calculates the sum of all numbers from 1 up to (and including) some number n

So for example, if n=3 we will get 6(1+2+3).

An example solution may be:

// first solution
function addUpTo(n) {
	let total = 0;
	for (let i = 1; i <= n; i++) {
		total += i;
	}
	return total;
}

Another example solution may be:

// second solution
function addUpTo(n) {
	return n * (n + 1) / 2;
}

As we can see here, the second solution is less intuitive compared to the first solution. This is because the second solution implements a mathematical logic.

The real question here is which one is better?. What does "better" mean in this context? Does "better" mean "faster?" or "less memory-intensive?". Let's focus on the two aforementioned points. Speed and memory intensity.

First, let's talk about speed. One method is to manually record the performance of our solution.

// both first and second solutions
...
 
var t1 = performance.now();
addUpTo(1000000000);
var t2 = performance.now();
console.log(`Time elapsed: ${(t2 - t1) / 1000} seconds`)

However, we will notice that if we run our code and measure the speed like this, it will vary each time we execute the function.

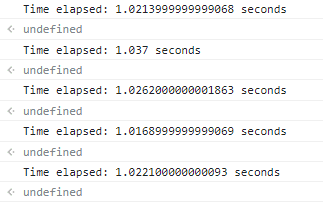
Every time we run the function, the time is different. Same applies for solution number 2.

We can clearly see the problem when measuring the quality of code by time.

• Different machines will record different times.
• Even the same machine will record different times!
• For fast algorithms, speed measurements may not be precise enough.

To solve the problem with time (ex. code takes too long to test) , big O notation comes into play.

Counting Operations

We have seen from above that counting the seconds, milliseconds is not precise enough as they vary. So what if we count the number of simple operations the computer has to perform instead?

What do we mean by "counting" operations? Let's take a look at the example below:

function addUpTo(n) {
	return n * (n + 1) / 2;
}

if we take a look at the function, there are 3 different operations taking place:

• 1 multiplication on *
• 1 addition on +
• 1 division on /

On the other hand, let's look at solution number 1:

function addUpTo(n) {
	let total = 0;
	for (i = 1; i <= n; i++) {
		total += i;
	}
	return total;
}

We can see that the number of operations this function goes through is different depending on the value of "n". If n=100 ...

• total += i is run 100 times as that line of code is inside a loop (which loops over 100 times). As total += i is equal to total = total + 1, we get 100 additions(+) and 100 assignments(=). That's 200 operations already!
• "100 times" is applied to other operations in the function as well.

Regardless of the exact number of operations, what's important is that the number of operations grow roughly proportionally with n.

Introduction to Big O

Big O notation is a way to formalize fuzzy counting. It allows us to talk formally about how the runtime of an algorithm grows as the inputs grow.

We say that an algorithm is O(f(n)) if the number of simple operations the computer has to do is eventually less than a constant times f(n), as n increases

• f(n) could be linear: f(n) = n
• f(n) could be quadratic (f(n) = 2^n)
• f(n) could be constant f(n) = 1
• f(n) could be something entirely different

Keep on thinking, 'as the n grows, what will the chart look like?'.

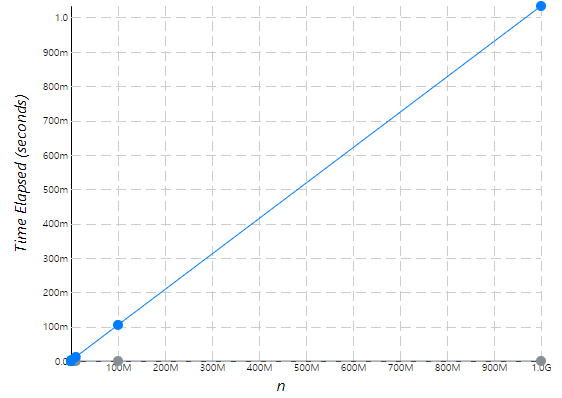
From the graph image above, the blue dots represent the results from solution 1 and the gray dots represent the results from solution 2.

Let's take a look at the second solution first. In the second solution, the graph is almost constant. In Korean, we could say that "기울기가 거의 일정함(the slope is not steep)". If this is the case, we could say that as "n" grows, it doesn't affect the operation runtime, thus giving us this result:

O(1)

However, the first solution is a bit different. The number of operations is bounded by a multiple of n (say, 5n). It doesn't matter if it's 5n or 10n, what matters is that it is a multiple of n (we simplify it to just n).

O(n)

Let's look at another example (count up and down):

// third example
function countUpaAndDown(n) {
	console.log("Going up!")
	for(let i = 0; i < n; i++) {
		console.log(i)
	}
	console.log("At the top! Going down")
	for(let j = n - 1; j >= 0; j--) {
		console.log(j)
	}
	console.log("At the bottom")
}

In this function, we have two for loops, which means that there are 2 O(n)s. However, instead of saying O(2n), we just say O(n) because as stated above, it doesn't matter if it's 5n or 10n, what matters is that it is a multiple of n.

O(n)

Let's look at a fourth example:

// fourth example
function printAllPairs(n) {
	for(let i = 0; i < n; i++) {
		for(let j = 0; j < n; j++) { // we have a nested loop!
			console.log(i, j)
		}
	}
}

So there's a loop inside a loop. We can say that O(n) operation is inside of an O(n) operation.

O(n^2)

Think of it as a 이차방정식(quadratic equation).

Simplifying Big O expressions

Depending on the function, the operations may add up to 2n or 10n. However, regardless of the exact number, the number of operations grows roughly proportionally with n.

When it comes to counting the number of operations, there are some rules when simplifying them.

1. Constants don't matter

• O(2n) (nope) -> O(n) (yes!)

• O(500) (nope) -> O(1) (yes!)

• O(20n^2) (nope) -> O(n^2) (yes!)

2. Smaller terms don't matter

• O(n + 10) (nope) to O(n) (yes!)

• O(1000n + 50) (nope) to O(n) (yes!)

• O(n^2 + 5n + 8) (nope) to O(n^2) (yes!) -> 5n + 8 is meaningless when compared with n^2.

Big O shorthands

There are several rules that can help when analyzing the complexity with Big O.

1. Arithmetic operations are constant

Whether we're adding something subtracting something, there's almost no difference when it comes to arithmetic operations. When we're doing 2 + 2 or 1000000 + 1000000, there's almost no difference in executing these operations.

2. Variable assignment is constant

x = 10000 and x = 10000000000 is roughly the same.

3. Accessing the elements in an array (by index) or object (by key) is constant

Literally.

4. In a loop, the complexity is the length of the loop times the complexity of whatever happens inside of the loop

refer to this code we've already seen above:

// fourth example
function printAllPairs(n) {
	for(let i = 0; i < n; i++) {
		for(let j = 0; j < n; j++) { // we have a nested loop!
			console.log(i, j)
		}
	}
}

Let's take a look at more examples.

// fifth example
function logAtLeast5(n) {
	for (let i = 1; i <= Math.max(5, n); i++) { // will loop to either "5" or "n", whichever is larger.
		console.log(i)
	}
}

So, what's the Big O of this function? Well, in the loop, i is either 5 or n. However, what we care about is the growth of n. When n grows and grows, 5 becomes irrelevant as n is so much bigger. So, we can say that the Big O of this function is this:

O(n)

What about this?

// sixth example
function logAtMost5(n) {
	for (let i = 1; i <= Math.min(5, n); i++) { // will loop to wither "5" or "n", whichever is smaller.
		console.log(i)
	}
}

In this case, it doesn't matter how big n is. If n is a miliion, the loop will run 5 times. If the n is 2, the loop will run 2 times.

O(1)

Space Complexity

Up until now, we discussed the speed of the execution of a function. In other words, Time Complexity. This brings up the question, 'how can we analyze the runtime of an algorithm as the size of the inputs increases?'.

We can also use Big O notation to analyze space complexity. 'How much additional memory do we need to allocate in order to run our code?'.

There are some rules of thumb when it comes to space complexity in javascript.

• Most primitive values are constant space (booleans, numbers, undefined, null)
• Strings require $O(n)$ space (where n is the string length)
• Reference types are generally $O(n)$, where n is the length (for arrays) or the number of keys (for objects)

Let's take a look at an example:

function sum(arr) {
	let total = 0;
	for(let i = 0; i < arr.length; i++) {
		total += arr[i]
	}
	return total;
}
 
console.log(sum([1, 2, 3, 4, 5])) // 15

So for this example, let's focus on the space, not the time.

• let total = 0 takes up a space of one number
• let i = 0 takes up a space of another number

Whether the length of arr is 100 or 1000, it doesn't really matter when considering the space taken up. We only have two variables and that's it. Of course we add new values to our total variable but that shouldn't be taken into account because the total variable is an already-existing variable. So, we could say...

O(1)

Here's another example:

function double(arr) {
	let newArr = [];
	for (let i = 0; i < arr.length; i++) {
		newArr.push(2 * arr[i]);
	}
	return newArr;
}
 
console.log(double([1, 2, 3, 4, 5])) // [2, 4, 6, 8, 10]

This example is different when comparing to the one above. The value newArr grows directly in proportion to the inserted arr value. For example, if the length of arr is 50, the length of newArr is also 50.

O(n)

Logarithms

We need to go over this topic as not all time and space complexities can be categorized to $O(1)$, $O(n)$, and $O(n^2)$. Sometimes, Big O expressions involve more complex mathematical expressions.

For a math dummy like me, let's simply go over what a log is.

$log_2(8) = 3 \to 2^3 = 8$

Here, we're simply asking ourselves, 2 to what power equals 8?. Let's make a simplified equation based on this:

$log_2(value) = e \to 2^e = value$

e = exponent

but for now, we'll omit the 2 because at the end of the day (when comparing the graphs), the 2 doesn't really make much of a difference.

$log === log_2$

So why is this important?

• Certain searching algorithms have logarithmic time complexity
• Efficient sorting algorithms involve logarithms
• Recursion sometimes involves logarithmic space complexity

At the end of the day, it's important to remember this graph - Logarithmic time complexity

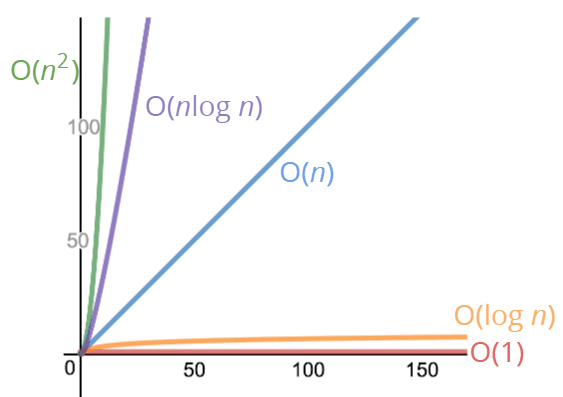
We can say that $O(log(n))$ is better than $O(n)$.

Recap

• To analyze the performance of an algorithm, we use Big O Notation
• Big O Notation can give us a high level understanding of the time or space complexity of an algorithm
• Big O Notation doesn't care about precision, only about general trends (linear? quadratic? constant?)
• The time or space complexity (as measured by Big O) depends only on the algorithm, not the hardware used to run the algorithm

Analyzing performance of arrays and objects

So we're going to briefly go over how objects and arrays work in the perspective of the Big O notation.

Objects

In javscript, data in objects are stored in key - value pairs and they are unordered.

You should use objects when...

• You don't need order
• You need fast access / insertion and removal

These are the Big Os of objects:

• Insertion - $O(1)$
• Removal - $O(1)$
• Searching - $O(n)$
• Access - $O(1)$

These are the Big Os of the Object Methods:

• Object.keys - $O(n)$
• Object.values - $O(n)$
• Object.entries - $O(n)$
• hasOwnProperty - $O(1)$

Arrays

In javascript, arrays are lists of ordered data.

You should use arrays when...

• When you need order
• When you need fast access / insetion and removal (sort of...)

These are the Big Os of arrays:

• Insertion - depends... If we try to push new data to the end of an array, it's going to be $O(1)$. However, if we try to push it to the first index, every data coming after the newly added data will need to be re-indexed (which will take a long time for long arrays). In this case, it would be $O(n)$ because we would have to do at least something once for every element.
• Removal - depends... Like above, if we try to remove data from the first index, every item coming after that must be re-indexed. Thus $O(n)$. Hoewver, removing an element from the end of an array will be $O(1)$.
• Searching - $O(n)$ - it will take longer to search for an element as the array grows longer.
• Access - $O(1)$ - No matter how long an index is, it's always constant. Let's say that the length of an array is 1000 and we need the key of the 900th data. Javascript isn't going to go over every single indices all the way up to 900. It's just going to go to the 900th index and give us the information.

These are the Big Os of the Array Methods:

Let's take a look at some of the Big O notations for array methods:

• push - $O(1)$ - pushing elements at the end of an array
• pop - $O(1)$ - removing elements at the end of an array
• shift - $O(n)$ - removes the first element from an array and returns that removed element
• unshift - $O(n)$ - adds one or more elements to the beginning of an array and returns the new length of the array
• concat - $O(n)$ - used to merge two or more arrays. This method does not change the existing arrays, but instead returns a new array.
• slice - $O(n)$ - returns a shallow copy of a portion of an array into a new array object selected from start to end (end not included) where start and end represent the index of items in that array. The original array will not be modified.
• splice - $O(n)$ - changes the contents of an array by removing or replacing existing elements and/or adding new elements in place.
• sort - $O(n * logN)$ - sorts the elements of an array in place and returns the reference to the same array, now sorted. The default sort order is ascending, built upon converting the elements into strings, then comparing their sequences of UTF-16 code units values.
• forEach/map/filter/reduce/etc. - $O(n)$ - looping over each element...

Long story short, objects are fast at almost everything but they don't have order while arrays have order but can take some time. If we were to use an array, it's best practice to add/remove from the end instead of the first.